 |
Amp Under Normal Operation |
Introduction
I. Ohm's Law
II. Watt's Law
III. What does this mean in regard
to 6 VDC to 12 VDC conversions?
IV. How does this affect heater blower
motors?
Questions or Comments?
Introduction
A common modification in early trucks is the conversion of the original
6 VDC system over to 12 VDC. Often this causes some confusion to the oletrucker
who is not familiar with the principles of DC electricity and current flow.
The easiest analogy is to compare the flow of current to that of
water flowing through a garden hose. The flow of current is similar to
the flow of the water through the hose, the voltage is similar to water
pressure, and the resistance is like the diameter of the hose that the
water is flowing through. For a given diameter garden hose if you increase
the water pressure (i.e. raise the voltage), you increase the water flow
(increase the current). If, on the other hand you kept the water pressure
the same but decreased the diameter of the garden hose (increasing the
resistance), you would reduce the water flow (reduce the current).
In electricity the principles stated above are represented mathematically by a formula known as Ohm's Law. Ohm's Law states that the voltage is equal to the current flowing through a circuit times the resistance of the circuit, or
E = I x R
| E | = Voltage (Volts DC) |
| I | = Current (Amps DC) |
| R | = Resistance (Ohms) |
Solving Ohms Law for the other variables yields:
| I = E / R | and | R = E / I |
Whenver energy is converted into another form there is some inefficiency. No circuit is 100% efficient. The wasted energy is dissipated as heat (power). As long as the dissipated power is within the design considerations of the circuit components there is no problem. When circuit designs considerations are exceeded conditions can arise which result in the destruction of circuit components due to excess power dissipation. Such excess conditions include increasing the operating voltage or current requirements of the circuit. Power dissipation can be determined by Watt's Law, which states
P = I x E
Where
| P | = Power (Watts DC) |
| I | = Current (Amps DC) |
| E | = Voltage (Volts DC) |
Solving Watts Law for the other variables yields:
| I = P / E | and | E = P / I |
another useful derivation of this formua is obtained by substituting
Ohm's Law (E=IxR) into Watt's Law which results in
P = I X I XR or
P = I2 x R
III. What does this mean in regard to 6 VDC to 12 VDC conversions?
Actually it's pretty simple, suppose you have a stock 1950 Chevrolet
3100 which came from the factory with a 6 VDC system. Let's also
suppose that our stock Chevy uses 60 watts of power when its running down
the road with headlights on, heater motor blowing, and radio playing.
Note that all my numbers are theoretical, I have no idea what the actual
amount of power used by such a setup would be. At any rate, by applying
Watt's Law from above
| I = P / E |
| I = 60 Watts / 6 VDC |
| I = 10 Amps DC |
we can determine that our Chevy is drawing 10 amps of current to keep
itself functioning. Now suppose we decide we are tired of that
old 6 V system and we want to upgrade to 12 VDC. After the installation
of the 12 V system we cruise down the road still using 60 Watts of power
but now we can calculate that
| I = P / E |
| I = 60 Watts / 12 VDC |
| I = 5 Amps DC |
So we cut our current requirements in half while still maintaining the
60 Watts in power that we needed to operate the vehicle. This is
one reason why automobile manufacturers changed from 6 VDC to 12 VDC.
The reduced current demand of the 12 V system allows them to use a smaller
gage of wire which is both cheaper and easier to work with.
Important Note
The above statement regarding half the current would only be
true assuming that all 6V devices (heater motors and light bulbs) were
replaced with 12V equivalents. If you are using the old 6V device
in conjunction with a voltage reducer then the affected circuit would actually
use twice the power that you did before because the device still uses the
same amount of power plus you have a voltage reducer dropping the other
6V from the 12V system.
IV. How does this affect heater blower motors?
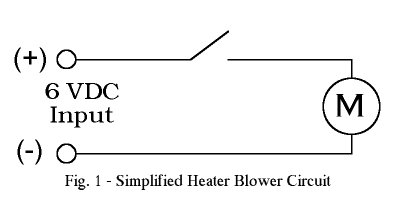
The circuit below (Fig. 1) is a simplified schematic of the heater blower circuit in a truck equipped with a 6V system.
 |
Amp Under Normal Operation |
When the switch is closed, the motor begins to operate and draws 1 amp
of current (hypothetical value). Since there are no other devices
in series with the motor in this circuit, the entire 6 V supply will be
applied across the motor terminals. With this information we can
calculated the effective load resistance of the motor using Ohm's Law from
above.
| R = E / I |
| R = 6 VDC / 1 Amp |
| R = 6 Ohms |
Now we know that our motor presents a 6 ohm load to the supply voltage.
We can also figure out how much power our motor uses from this information.
For this calculation we use Watt's Law.
| P = I2 x R |
| P = 1 Amp2 x 6 Ohms |
| P = 6 Watts |
So our motor uses 6 Watts of power under normal operation.
Suppose we convert to a 12 VDC system without making any modifications
to the blower motor circuit. This would result in the the circuit
shown below (Fig. 2).
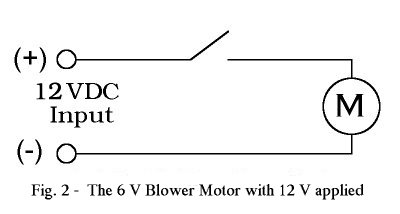 |
Has An Effective Resistance of 6 Ohms |
Calculating the amp draw of the motor under this condition yields
| I = E / R |
| I = 12 VDC / 6 Ohms |
| I = 2 Amps |
and taking that and calculating power we find
| P = I2 x R |
| P = 2 Amps2 x 6 |
| P = 24 Watts |
So we find under these circumstances that we
are drawing twice the current we would under normal circumstances and dissipating
4 times the power!! The motor would quickly fail unless
something is added to the circuit to bring it back into normal operating
parameters.
That something is what is commonly called the voltage reducer.
In actuality it is nothing more than a resistor which is designed to have
a voltage drop across it of 6 VDC. The schematic below illustrates
the same blower motor circuit with a voltage reducer installed.
 |
Has An Effective Resistance of 6 Ohms and Voltage Reducer has a voltage drop of 6 VDC. |
Now that we have installed the voltage reducer with it's 6 V drop the other 6 Volts is dropped across the motor. Note that the voltage reducer must have the same resistance value as the effective resistance of the motor in order to drop the voltage to the required 6 VDC. The motor is now operating at the voltage and current it was designed for while the reducer dissipates the remaining power in the circuit.
Questions or Comments? Email Me
Bill Bailey
Last Revised : 8/15/99
Thanks to Brad Rusnak for his comments concerning this write-up